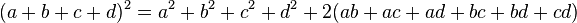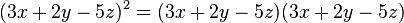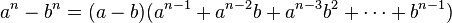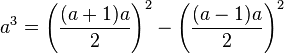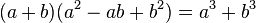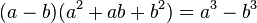Productos Notables

Cubo de la diferencia de dos terminos

Es igual al cubo del primer termino menos el triple producto del cuadrado del primer termino por el segundo mas el triple producto del primer termino por el cuadrado del segundo menos el cubo del segundo

( 6x - 2y )³

(6x)³

3(6x)²(2y)

3(6x)(2y)²

(2y)³

a) El cubo del 1er término es (6x)(6x)(6x) = 216x³

b) El triple del cuadrado del primer término por el segundo término

3(6x)(6x)(2y)=(18x)(6x)(2y)=(108x²)(2y)=(216x²y)

c) El triple del primer término por el cuadrado del segundo término

3(6x)(2y)(2y)=(18x)(2y)(2y)=(36xy)(2y)=(72xy²)

d) El cubo del 2do término es (2y)(2y)(2y) = 8y³

Entonces

( 6x - 2y )³

216x³

216x²y

72xy²

8y³

Cuadrado de un polinomio

Para elevar un polinomio de cualquier cantidad de términos se suman los cuadrados de cada término individual y luego se añade el doble de la suma de los productos de cada posible par de términos.

(a+b+c)^2 = a^2 +b^2+c^2 + 2(ab+ac+bc) \,

(a+b+c+d)^2 = a^2 +b^2+c^2 + d^2+ 2(ab+ac+ad+bc+bd+cd) \,

Ejemplo:

(3x+2y-5z)^2 = (3x+2y-5z)(3x+2y-5z) \,

Diferencia de potencias enésimas

Diferencia de potencias enésimas:

a^n-b^n = (a-b)(a^{n-1} + a^{n-2}b + a^{n-3}b^2 +\cdots + b^{n-1}) \,

Las fórmulas de binomio al cuadrado y binomio al cubo se pueden generalizar mediante el teorema del binomio.

Para representar el cubo de un monomio, como diferencia de dos cuadrados, existe una fórmula ingeniosa:

a^3 = \left(\frac{(a+1)a}{2}\right)^2 - \left(\frac{(a-1)a}{2}\right)^2

Otras identidades...

Dado que la notabilidad de un producto es un concepto ambiguo, no existe una lista determinante que indique a cuáles productos se les puede considerar notables, y a cuáles no. A otras fórmulas, aunque menos usadas que las anteriores, en ciertos contextos se les puede calificar de productos notables. Entre ellas se destacan:

Adición de cubos:

a^3+b^3 = (a+b)(a^2-ab+b^2) \,

Diferencia de cubos:

a^3-b^3 = (a-b)(a^2+ab+b^2) \,

Es más frecuente listar las dos expresiones anteriores como las fórmulas de factorización, ya que los productos no tienen una forma particularmente simétrica, pero el resultado sí (contrástese, por ejemplo, con la fórmula de binomio al cubo).

(a+b)(a^2-ab+b^2) = a^3+b^3 \,

(a-b)(a^2+ab+b^2) = a^3-b^3 \,

La suma y la diferencia de cubos se pueden generalizar a sumas y diferencias de potencias enésimas (o n - ésimas: xⁿ).

Producto Notables

Producto notable

La noción de productos notables, sin embargo, no suele referirse a esta cuestión, sino que se emplea en la matemática para nombrar a determinadas expresiones algebraicas que pueden factorizarse de manera inmediata, sin recurrir a un proceso de diversos pasos.

En este sentido, debemos recordar que el concepto de producto, en el ámbito matemático, refiere al resultado de una operación de multiplicación. Los valores que entran en juego en estas operaciones, por otra parte, se conocen como factores.

Una expresión algebraica que aparece con frecuencia y que puede someterse a una factorización a simple vista, por lo tanto, se denomina producto notable. Un binomio cuadrado y el producto de dos binomios conjugados son ejemplos de productos notables.

Un ejemplo concreto de producto notable es el siguiente:

(m + n)² = m² + 2mn + n²

Dicho producto notable refiere que el cuadrado de la suma de m y n es igual al cuadrado de m más dos veces m multiplicado por n más el cuadrado de n.

Lo podemos comprobar reemplazando los términos por valores numéricos:

(2 + 4)² = 2² + 2 x 2 x 4 + 4²

6²= 4 + 16 + 16

36 = 36

De esta manera, si nos encontramos el cuadrado de un binomio como en el ejemplo anterior, podemos factorizarlo de manera inmediata, sin necesidad de recurrir a todos los pasos, ya que se trata de un producto notable.