Dado que la notabilidad de un producto es un concepto ambiguo, no existe una lista determinante que indique a cuáles productos se les puede considerar notables, y a cuáles no. A otras fórmulas, aunque menos usadas que las anteriores, en ciertos contextos se les puede calificar de productos notables. Entre ellas se destacan:
Adición de cubos:
Diferencia de cubos:
Es más frecuente listar las dos expresiones anteriores como las fórmulas de factorización, ya que los productos no tienen una forma particularmente simétrica, pero el resultado sí (contrástese, por ejemplo, con la fórmula de binomio al cubo).
La suma y la diferencia de cubos se pueden generalizar a sumas y diferencias de potencias enésimas (o n - ésimas: xn).


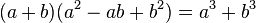
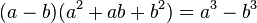
No hay comentarios:
Publicar un comentario